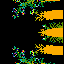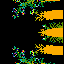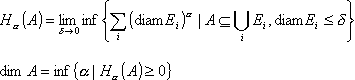Существует большое число математических объектов называемых фракталами: треугольник Серпинского, снежинка Коха, кривая Пеано, множество Мандельброта, лоренцевы аттракторы. Фракталы с большой точностью описывают многие физические явления и природные образования: горы, облака, турбулентные течения, корни, ветви и листья деревьев, кровеносные сосуды, что далеко не соответствует простым геометрическим фигурам. Впервые фрактальную природу нашего мира подметил математик Бенуа Мандельброт:
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в ее неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. Природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности." MB2

   Согласно Мандельброту, слово фрактал происходит от латинских слов fractus - дробный и frangere - ломать, что отражает суть фрактала, как "изломанного", нерегулярного множества MB2,стр.4. Мандельброт дал строгое математическое определение фрактала, как множества, хаусдорфова размерность которого, строго больше топологической размерности. Он однако так и не был удовлетворен этим определением, так как оно не включает в себя некоторые множества, рассматриваемые многими математиками, как фракталы.

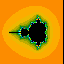
   В 1991 году М.Шишикура SH доказал любопытный факт: Хаусдорфова размерность границы широко известного множества Мандельброта в точности равна двум!

---

   Кубическая размерность (box dimension) является несколько более простым понятием. Если A некоторое компактное множество, и N(r) есть минимальное число шаров радиуса r покрывающих A, и если существует предел lim( log N(r)/ log (1/r) ), при r стремящемся к нулю, то этот предел называется кубической размерностью множества A. Известно, что Хаусдорфова размерность не превосходит кубическую, а для самоподобных фракталов (см. ниже) они совпадают.

---

   Топологическая размерность, принимая исключительно целые значения, согласуется с интуитивным представлением о размерности множества. Так размерность одноточечного множества равна нулю, отрезка и прямой - единица, ... размерность n-мерного куба равна n. Более строго:
  Топологическая размерность множества A равна нулю, если для любой точки множества A найдется сколь угодно малая окрестность, граница которой не пересекается с A;
  Топологическая размерность A равна n, если для любой точки этого множества найдется сколь угодно малая окрестность, граница которой пересекается с A по множеству размерности n-1, и кроме того n есть наименьшее положительное число для которого это условие выполнено.

---

   Строгое определение самоподобных множеств было дано Дж.Хатчинсоном в его ставшей уже классической статье 1981 года HJ. Множество F Хатчинсон назвал самоподобным, если оно состоит из нескольких компонент, подобных F (т.е компонент получаемых поворотом, сжатием и отражением множества F). Стоит оговориться, что оригинальное определение Хатчинсона немного сложнее, но современные математики все чаще пользуются именно этим.
  Примеры самоподобных множеств:

Приведу ключевую теорему из статьи Хатчинсона
  Теорема: Если S₁,..,S_N - набор сжимающих отображений полного метрического пространства X на себя, то найдется единственное замкнутое множество F, такое что F=S₁(F)U..U S_N(F). Более того, множество F - компакт.
   Множество F из теоремы называют инвариантным множеством системы сжимающих отображений или IFS-множеством (Iterated Function System) и обозначают F=IFS(X;S₁,..,S_N). В качестве пространства X обычно рассматривают n-мерное пространство Rⁿ. Если все отображения S_i являются аффинными сжатиями, то соответствующее инвариантное множество называют самоаффинным.

---

   Самоподобные и самоаффинные фракталы строят простым и быстрым алгоритмом итераций отображений подобия. Среди изображений построенных компьютером встречаются естественно выглядящие картины растений и деревьев. Пусть {S₁,..,S_N} - некоторая система аффинных сжатий. Отображения S_i представимы в виде: S_i(x)=A_i( x-o_i )+o_i, где A_i - фиксированная матрица размера 2x2 и o_i - двумерный вектор столбец.